One of the central problems in modern solid-state physics is the problem of the so-called Strongly Correlated Systems. In order to understand what it is, we need to dive a little bit into the basics modern condensed matter physics. The main idea that forms the core of the field is that the excitation spectrum of a generic complex many-body system can be represented as a collection of independent “quasiparticles”. The remaining degrees of freedom (e.g. lattice) are assumed to merely provide a background for the freely moving quasiparticles. This is commonly referred to as the “Landau framework” and despite its apparent simplicity, it has been extremely successful in describing the overwhelming majority of observed phenomena in condensed matter physics. However, as general as Landau framework is, there are physical systems that apparently fall beyond it; collectively they are referred to as “Strongly Correlated Systems”.
The problem of Strongly Correlated Systems mentioned above is the lack of a unifying description comparable to the intuitive quasiparticle picture of the conventional many-body systems. Recent developments have suggested there exist an unexpected novel principle in many-body physics stating that there exists an upper limit on the scattering rate determined solely by temperature
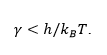
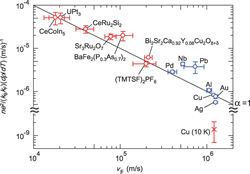
According to the hypothesis this so-called Planckian scattering rate cannot be exceeded in principle, and this limit is saturated in strongly correlated systems.
This Planckian hypothesis proposes a new fundamental principle for matter organization, but proving it is challenging. The idea of the Planckian limit was suggested by traditional methods such electrical transport, but these techniques do not provide direct access to the scattering rates.
To address this, we have developed an innovative technique that combines intense, single-cycle THz pulses with an ultrafast transient grating setup, allowing us to achieve sub-micron spatial resolution. The goal of the experiment is to provide a definitive experimental evidence for the existence of the ultimate Planckian limit in condensed matter systems (or the lack thereof).
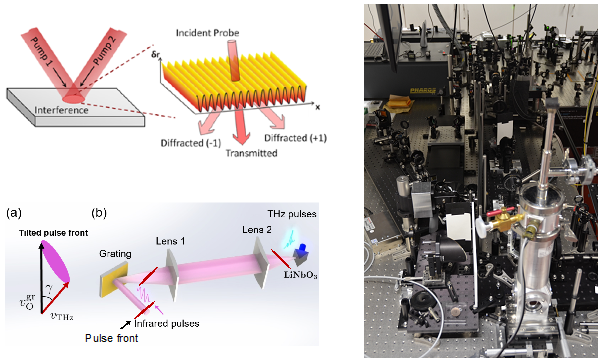
Bottom left: an illustration of the “tilted wave-front” technique to generate intense THz pulses by means of frequency conversion of near-infrared pulses inside nonlinear optical crystal. The resulting THz pulses come out as ultrashort (~1picosecond (ps)) and ultra-strong (~500kV/cm peak amplitude) pulses that can be used to e.g. manipulate the transient grating to observe to sub-micron and sub-ps transport or to induce non-linear THz response with multiple pulses (2D THz; see other projects); Right: real-life incarnation of the setup combining tilted-wavefront-generated THz source (left half) and a transient grating setup (right half), while the sample being placed inside an optically-accessible liquid He cryostat (the aluminum thing in the foreground).
